Model Extraction, LLM Abuse, and Covert Learning Algorithms: Exploring Provable Security

This is part 2 of a 3-part (Part 1, Part 3 -- coming soon) blog post which is in part based on my papers [CK21] and [Kar23], which appeared at TCC '21 and SaTML '23, respectively.


Covert learning attacks

In part 1 of this blog series, we introduced the model extraction scenario first, and then give an overview of a specific type of model extraction defense, which called an Observational Model Extraction Defense (OMED), focusing on the theoretical underpinnings of these defenses. We then outlined the techincal contributions of [Kar23], which, briefly speaking, cast a lot of doubt on whether or not these OMEDs can provide any provable security guarantees against the model extraction problem. In part 2 of the blog series (this blog post), we will dig into what exactly is Covert Learning [CK21] --- the mysterious learning algorithm that lay at the center of the results of [Kar23] for impossibility of efficiently defending against model extraction attacks using OMEDs.

Let's dive into the connection between model extraction in the presence of OMEDs, and the Covert Learning model [CK21]. This blog post will assume a basic familiarity with computational learning theory, and specifically, the Probably Approximately Correct (PAC) learning model.

The Covert Learning model is a variant of Valiant's PAC-learning model, in the agnostic learning with queries setting. In agnostic learning with queries, a learning algorithm has access to an oracle that labels points in the domain of the target concept. These points can be chosen arbitrarily by the learning algorithm. In the "agnostic" setting, the goal is for the learning algorithm to identify a model (within some predifined "touchstone" class) that approximates an arbitrary target concept implemented by the oracle approximately as well as the best possible model contained in the touchstone class. The agnostic setting mirrors the way machine learning is traditionally conducted in practice (as opposed to the "realizable" setting, where the target concept is assumed to be contained by a predefined concept class).

The point of the Covert Learning model is to formalize a new type of privacy in learning theory. Specifically, Covert Learning algorithms provide the guarantee that the queries leak very little information about the concept, with respect an adversary that can take a look at the queries. In this way, the Covert Learning algorithm gets privacy for what it is learning.

In other words, Covert Learning allows one to learn a concept (using knowledge of some internal randomness only known to itself),[1] while the adversary remains nearly completely "in the dark" about the concept, even given a view of the entire transcript of membership queries and oracle responses. Crucially, the adversary is not privy to the secret randomness of the learning algorithm.

Covert Learning Depiction
Figure 2: A depiction of natural Covert Learning. A learning algorithm queries an oracle for a concept at points of it's choice, with the goal of obtaining an approximation to the concept. Meanwhile, an eavesdropping adversary obtains a transcript of the interaction with the oracle and tries to distinguish the transcript from a set of random examples.


"the Covert Learning algorithm gets privacy for what it is learning."



An example we can use to build intuition about what Covert Learning is all about is the following. Imagine being in a course, with one teacher and many classmates, where you are graded "on a curve" (meaning the goal is to finish ranked first in the class). To do this, you need to learn the day's concept by asking questions of the teacher (for simplicity, restrict to "yes or no" questions). The catch is that every one of your classmates gets to observe your questions and the teacher's answers. Can you design questions a unique set of questions that allows you to learn the day's concept, but prevent all your classmates from learning the concept similarly as well? Covert Learning algorithms provide a solution to this problem, under some natural assumptions (to be explained later).

So, how do we model such a question in a mathematical way? Covert Learning does this by borrowing from the Simulation-based security paradigm from the field of Cryptography.

Roughly speaking, any membership query learning algorithm is a Covert Learning algorithm if it has an accompanying simulator (i.e., a polynomial time algorithm) which, when given access only to random examples, emulates the distribution over the membership queries used by the Covert Learning algorithm in a computational indistinguishable way. In other words, the simulator is able to produce a "believable" transcript of the interaction between the learning algorithm and the query oracle, without query access to the underlying concept, but only (for instance) uniformly random examples.

For a concept class where access only to uniformly random examples makes learning computationally hard, this proves that the learning transcript reveals very little information to a computationally bounded adversary. Loosely speaking, this comes from the following logic:

  1. the existence of the simulator shows that the distribution over the queries is hard to distinguish from a distribution that can be efficiently derived from uniformly random examples
  2. if there was an adversary that could learn some information about the concept from those queries, then that adversary could act as a distinguisher.

These two points together are in contradiction, so we conclude that any adversary can't obtain any knowledge about the concept from the queries. Hence, Covert Learning algorithms are reserved for concept classes that are not (known to be) efficiently learnable in the original PAC-model with respect to a certain "hard example distribution." There are many such concept classes, such as decision trees and low-depth neural networks, which have so far evaded the computational learning theory communities attempts at designing polynomial time PAC learning algorithms.

Now I want to highlight a special case of Covert Learning, called natural Covert Learning, which is often easier to think about than the simulation-based version. In Natural Covert Learning, rather than requiring a simulator for the query interaction, we require that the distribution over the membership queries is computationally indistinguishable from a single pre-defined "hard example distribution." For concreteness, let us consider the uniform distribution as the pre-defined "hard distribution." Also, in Natural Covert Learning we will consider the realizable learning PAC setting (rather than agnostic).

Connecting Covert Learning to Model Extraction with OMEDs

Now we're finally ready to draw the connection between (Natural) Covert Learning, and the model extraction problem.

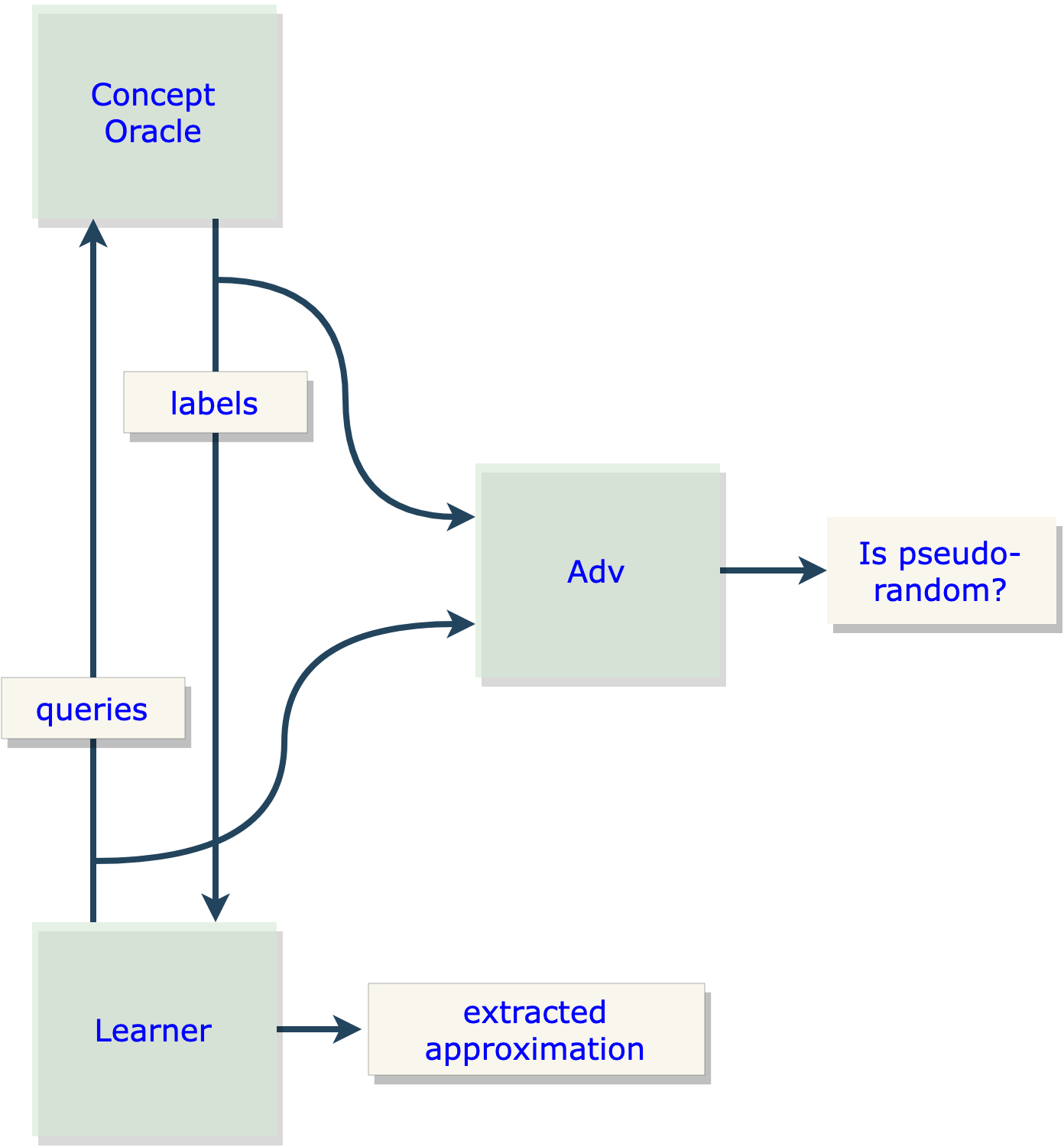
The adversary in natural Covert Learning --- a distinguisher that attempts to distinguish the membership queries made by the learner algorithm from random examples, is essentially the "adversary" in a model extraction attack --- an OMED.

At first glance this sounds really confusing, because normally the adversary in model extraction is supposed to be the malicious client that is trying to reverse engineer the model. However, consider that the job of the OMED is to somehow distinguish benign clients from adverse clients. Thus, thinking from the perspective of the actual adversary (i.e., the model extractor), the OMED is adversarial in nature and has essentially the same job as the natural Covert Learning adversary: to detect some property about the client's distribution of queries. This becomes even more apparent when considering the similarities between Figure 1 (see Blog post 1) and Figure 2.

By exploiting this connection, we can actually demonstrate that natural Covert Learning algorithms form a recipe for an attack that can fool the OMED in the same way that they fool the Covert Learning adversary. Plus, the Learning guarantee of natural Covert Learning then allows us to still argue that the client can extract the underlying model. Hence, we can show that a single Covert Learning attack can achieve extraction while "fooling" any OMED. That is, any OMED will output "accept" with high probability even though an extraction attack is being performed.


"The adversary in natural Covert Learning --- a distinguisher that attempts to distinguish the membership queries made by the learner algorithm from random examples, is essentially the "adversary" in a model extraction attack --- an OMED."



Conclusion: on the need for Covert Learning instead of PAC-learning

To wrap up part 2 of this blog series, I want to hammer home the point about exactly why and how Covert Learning algorithms are at the crux of model extraction attacks in the presence of OMEDs. We touched on the fact that all models are at risk of extraction by the very fact that they are exposed by some interface. Again, the VC dimension argument outlined in part 1 of the blog series shows that, given enough even uniformly random examples of the input/output behavior of the model, and enough computational power, an adversary has a PAC-learning algorithm that would work for extraction. . Additionally, since the PAC-learning algorithm only uses random examples, then the model extraction adversary can choose to make queries according to a distribution that is "accepted" by the OMED.

However, the VC dimension argument in general relies on unbounded computational power, but only very simple concept classes are known to be PAC-learnable in polynomial time from random examples (e.g., linear models). Hence, the natural question is whether there exists effective model extraction defenses against polynomial time adversaries, as is customary in Modern Cryptography. Again, this is because many important models (e.g. decision trees, low-depth neural networks) are not known to be PAC-learnable in polynomial time (on the uniform distribution over discrete inputs, say). On the other hand, a class like decision trees is learnable in polynomial time when using carefully synthesized queries. But, classic membership query algorithms like the Kushilevitz-Mansour algorithm [KM93] (which is used to learn decision trees in polynomial time) make queries that can be tested and identified as problematic by the OMED.

Therefore, Covert Learning algorithms bridge the gap between these two settings; the Covert Learning algorithms constitute attacks that are benign-looking, but are actually adverse. In other words, they are polynomial time membership query PAC-learning algorithms that synthesize queries in a special way that is provably hard to distinguish from the classic PAC-learning with random examples setting. This means that Covert Learning attacks are both undetectable by an (efficient) OMED, and run in polynomial time. On the other hand, The VC dimension argument is undetectable by the OMED, but is not efficient, while the membership query attack by [KM93] is efficient, but is detectable by the OMED.

[1] Note that, the internal randomness is not even shared with the concept oracle. To use an analogy from Cryptography, Covert Learning is "public-key" in nature, as opposed to "symmetric-key," which might rely on shared randomness between the learner and the concept oracle.

References


[BCK+22] Eric Binnendyk, Marco Carmosino, Antonina Kolokolova, Ramyaa Ramyaa, and Manuel Sabin. Learning with distributional inverters. In International Conference on Algorithmic Learning Theory, pages 90–106. PMLR, 2022.
[BFKL93] Avrim Blum, Merrick Furst, Michael Kearns, and Richard J Lipton. Cryptographic primitives based on hard learning problems. In Annual International Cryptology Con- ference, pages 278–291. Springer, 1993.
[CCG+20] Varun Chandrasekaran, Kamalika Chaudhuri, Irene Giacomelli, Somesh Jha, and Song- bai Yan. Exploring connections between active learning and model extraction. In 29th {USENIX} Security Symposium ({USENIX} Security 20), pages 1309–1326, 2020.
[CJM20] Nicholas Carlini, Matthew Jagielski, and Ilya Mironov. Cryptanalytic extraction of neural network models. arXiv preprint arXiv:2003.04884, 2020.
[CK21] Ran Canetti and Ari Karchmer. Covert learning: How to learn with an untrusted intermediary. In Theory of Cryptography Conference, pages 1–31. Springer, 2021.
[CLP13] Kai-Min Chung, Edward Lui, and Rafael Pass. Can theories be tested? a cryptographic treatment of forecast testing. In Proceedings of the 4th conference on Innovations in Theoretical Computer Science, pages 47–56, 2013.
[DKLP22] Adam Dziedzic, Muhammad Ahmad Kaleem, Yu Shen Lu, and Nicolas Papernot. In- creasing the cost of model extraction with calibrated proof of work. arXiv preprint arXiv:2201.09243, 2022.
[GBDL+16] Ran Gilad-Bachrach, Nathan Dowlin, Kim Laine, Kristin Lauter, Michael Naehrig, and John Wernsing. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In International Conference on Machine Learning, pages 201–210. PMLR, 2016.
[GL89] Oded Goldreich and Leonid A Levin. A hard-core predicate for all one-way functions. In Proceedings of the twenty-first annual ACM symposium on Theory of computing, pages 25–32, 1989.
[GMR89] Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof systems. SIAM Journal on computing, 18(1):186–208, 1989.
[GPV08] Craig Gentry, Chris Peikert, and Vinod Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the fortieth annual ACM sym- posium on Theory of computing, pages 197–206, 2008.
[JCB+20] Matthew Jagielski, Nicholas Carlini, David Berthelot, Alex Kurakin, and Nicolas Paper- not. High accuracy and high fidelity extraction of neural networks. In 29th {USENIX} Security Symposium ({USENIX} Security 20), pages 1345–1362, 2020. 25
[JSMA19] Mika Juuti, Sebastian Szyller, Samuel Marchal, and N Asokan. Prada: protecting against dnn model stealing attacks. In 2019 IEEE European Symposium on Security and Privacy (EuroS&P), pages 512–527. IEEE, 2019.
[Kar23] Ari Karchmer. Theoretical limits of provable security against model extraction by efficient observational defenses. In 2023 IEEE Conference on Secure and Trustworthy Machine Learning (SaTML), pages 605–621. IEEE, 2023.
[KM93] Eyal Kushilevitz and Yishay Mansour. Learning decision trees using the fourier spec- trum. SIAM Journal on Computing, 22(6):1331–1348, 1993.
[KMAM18] Manish Kesarwani, Bhaskar Mukhoty, Vijay Arya, and Sameep Mehta. Model extrac- tion warning in mlaas paradigm. In Proceedings of the 34th Annual Computer Security Applications Conference, pages 371–380, 2018.
[KST09] Adam Tauman Kalai, Alex Samorodnitsky, and Shang-Hua Teng. Learning and smoothed analysis. In 2009 50th Annual IEEE Symposium on Foundations of Computer Science, pages 395–404. IEEE, 2009.
[Nan21] Mikito Nanashima. A theory of heuristic learnability. In Conference on Learning Theory, pages 3483–3525. PMLR, 2021.
[O’D14] Ryan O’Donnell. Analysis of boolean functions. Cambridge University Press, 2014.
[PGKS21] Soham Pal, Yash Gupta, Aditya Kanade, and Shirish Shevade. Stateful detection of model extraction attacks. arXiv preprint arXiv:2107.05166, 2021.
[Pie12] Krzysztof Pietrzak. Cryptography from learning parity with noise. In International Conference on Current Trends in Theory and Practice of Computer Science, pages 99–114. Springer, 2012.
[PMG+17] Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. Practical black-box attacks against machine learning. In Proceed- ings of the 2017 ACM on Asia conference on computer and communications security, pages 506–519, 2017.
[RWT+18] M Sadegh Riazi, Christian Weinert, Oleksandr Tkachenko, Ebrahim M Songhori, Thomas Schneider, and Farinaz Koushanfar. Chameleon: A hybrid secure compu- tation framework for machine learning applications. In Proceedings of the 2018 on Asia Conference on Computer and Communications Security, pages 707–721, 2018.
[TZJ+16] Florian Tram`er, Fan Zhang, Ari Juels, Michael K Reiter, and Thomas Ristenpart. Stealing machine learning models via prediction apis. In 25th {USENIX} Security Symposium ({USENIX} Security 16), pages 601–618, 2016.
[Vai21] Vinod Vaikuntanathan. Secure computation and ppml: Progress and challenges. https: //www.youtube.com/watch?v=y2iYEHLY2xE&ab_channel=TheIACR, 2021.
[YZ16] Yu Yu and Jiang Zhang. Cryptography with auxiliary input and trapdoor from constant-noise lpn. In Annual International Cryptology Conference, pages 214–243. Springer, 2016.