Model Extraction, LLM Abuse, and Covert Learning Algorithms: Exploring Provable Security

This is part 1 of a 3-part (Part 2, Part 3 -- coming soon) blog post which is in part based on my papers [CK21] and [Kar23], which appeared at TCC '21 and SaTML '23, respectively.


Consider LLM chatbots like OpenAI's ChatGPT or Anthropic's Claude. Could a long conversation with ChatGPT be enough to "clone" it? Said differently, could someone get to know Claude so well, that they could program "Claudio," who performs a reasonable impersonation of Claude?

In a model extraction attack, more generally, an adversary maliciously probes an interface to a machine learning (ML) model in an attempt to extract the ML model itself. Model extraction was first introduced as a risk by Tramer et al. [TZJ+16], at USENIX `16.

(An imaginative depiction of Claude meeting Claudio.)

Besides impersonating chatbots, having an ML model stolen is a risk whenever interaction with the model is allowed, like in any machine learning as a service (MLaaS) scenario. So, let's highlight two main concerns that summarize why we need to seriously care about the model extraction scenario.


In part 1 of this series, I'm going to spend more time introducing the model extraction scenario first, and then give an overview of a specific type of model extraction defense, which I call an Observational Model Extraction Defense (OMED), with a focus on giving my interpretation of some of the theoretical underpinnings of these defenses. After that, I'll describe the techincal contributions of [Kar23], which serve to cast a lot of doubt on whether or not these OMEDs can provide any provable security guarantees against the model extraction problem.

Contents

Defending against model extraction

So, clearly, maintaining the preventing model extraction is important. Understanding how to defend against model extraction has been considered (see e.g. the papers [KMAM18][TZJ+16][CCG+20][JMAM19][PGKS21]).

Most model extraction defenses (MEDs) existing in the academic literature belong to two types.

In this blog post, we will not focus on the noisy responses defense, because it necessarily sacrifices predictive accuracy of the ML model. In general, defenses are all about balancing security against model extraction with accuracy. The noisy responses defense sacrifices accuracy in favor of security against model extraction in a strong way, and may not be a viable option at all for many ML systems where accuracy is critical such as autonomous driving, medical diagnosis, or malware detection.

OMEDs

OMEDs, on the other hand, totally pereserve accuracy, since they do not change the underlying model.

A common implementation of the observational defense involves a so-called "monitor" that takes as input a batch of requests submitted by the client and computes some statistic that measures the likelihood of adversarial behavior. The goal is to reject a client's requests when the queries pass a certain threshold on the statistic. Some examples of proposals following this template are [KMAM18][JMAM19] and [PGKS21].

Essentially, observational defenses aim to control the distribution of the client's queries. They do this by classifying any clients that fail to conform to the appropriate distributions as adverse, and then prohibiting them from accessing the model. See Figure 1 below.

Model Extraction Depiction
Figure 1: A depiction of the model extraction setting in the presence of an OMED. The adverse client queries the ML model, attempting to extract an approximation. The OMED watches over the interaction and outputs a decision to accept (and forward the labels) or reject the client based on whether or not it is deemed adverse or benign.

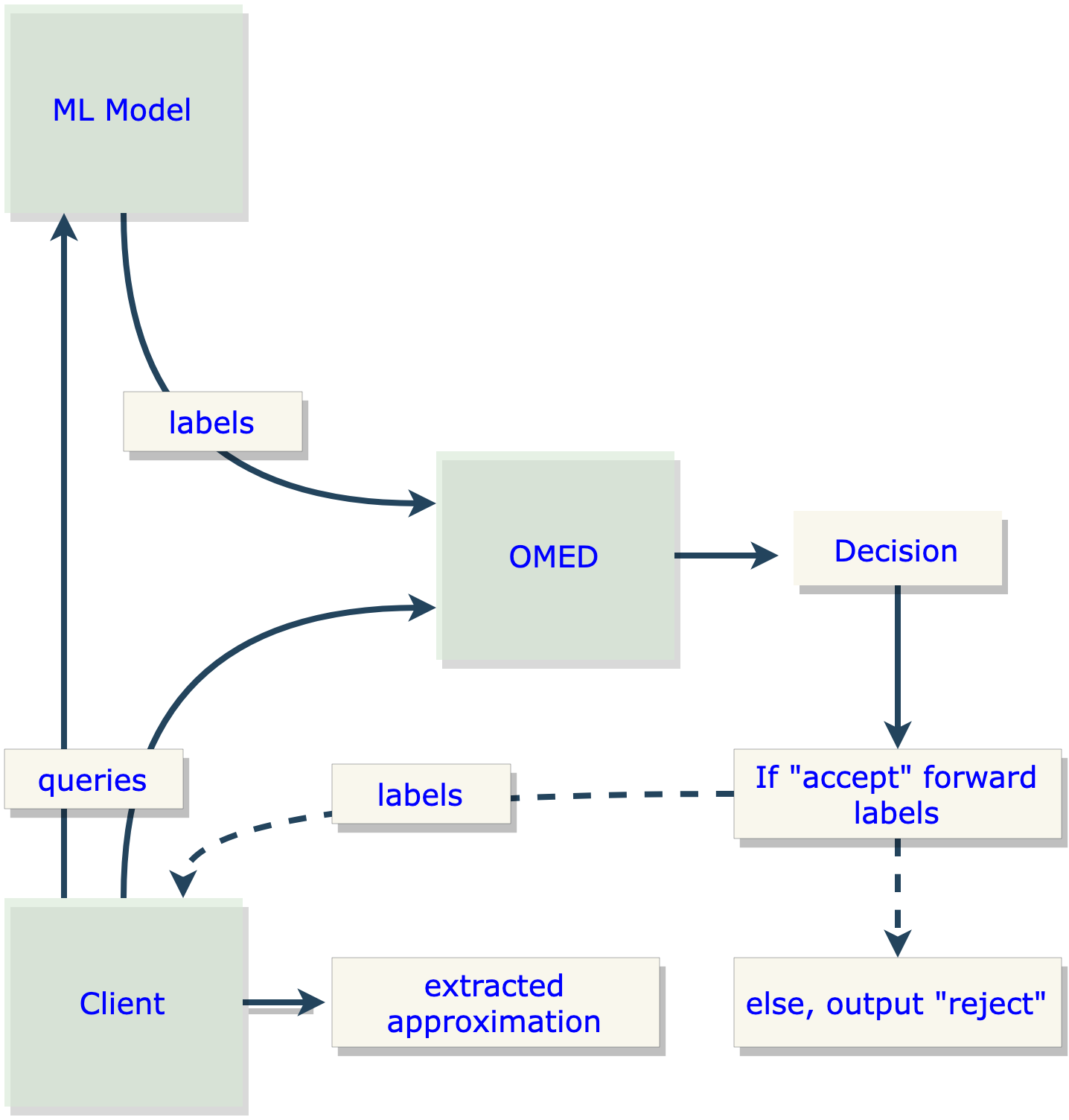
Said differently, any client that wishes to interact with the ML model, adverse or benign, must query according to an acceptable distribution, since if they do not the OMED will refuse service.

This prompts the question: how should we choose the appropriate acceptable distributions? To date, the choice of such distributions has been made heuristically. For instance, in [JMAM19], an acceptable distribution is one with the property that the distribution over hamming distances between queries is normally distributed.

However, no formal definitions of security against model extraction have even been suggested. Neither has there been much formal work done to understand the theoretical underpinnings of the observational defenses proposed in the literature. In fact, this was highlighted by Vinod Vaikuntanathan as an open problem in his talk at the Privacy Preserving Machine Learning workshop at CRYPTO '21.

As a result, a "cat-and-mouse" progression of attacks and defenses has developed, while no satisfying guarantees have been discovered ("for neither cat nor mouse").

Towards provable security against model extraction

In my recent paper [Kar23], we consider whether OMEDs can have satisfying provable guarantees of security. We are inspired by the modern theory of Cryptography, where the security of some protocol is mathematically guaranteed by the infeasibility of some very hard computational problem.

But, how do we even define security against model extraction? An initial attempt could try to leverage zero-knowledge style security. Zero-knowledge proofs and their simulation-based security can make up another blog post (or an entire textbook); but, essentially, a zero-knowlege guarantee would say that a client learns nothing about the ML model that they could not have already learned prior to the interaction with the model. Hence, the client learned nothing about the model from its queries.

This sounds great. However, it is too strong of a security goal: at the very least the client will learn some queried examples. For example, if we imagine the MLaaS setting, the client must be granted at least some ability to learn information ("in good faith"). Otherwise, the client may take business elsewhere, or not use the model at all.

What kind of zero-knowledge guarantees could we feasibly hope to obtain, then? One possible revised goal, could be to guarantee that a client learns zero knowledge beyond whatever they could learn from a set of random queries on the model. This privilege constitutes a middle ground between the too restrictive fully zero-knowledge guarantee, and allowing a client total query access to the model.

An implicit model of security for OMEDs

One of the most important observations of my paper [Kar23] is that, in fact, this notion of security appears to be implicitly behind existing OMEDs! The literature on OMEDs tends to cite the goal of detecting model extraction, but the downstream effect is that the observational defenses seek to exactly confine the queries obtained by the client to some specific distributions (by enforcing a particular benign behavior). The benign behavior is enforced because the OMED will reject the client's queries if their distribution fails some chosen statistical test. Hence, the idea of only serving clients confined to these benign query distributions undoubtedly assumes that whatever can be deduced about the model by a benign client using queries sampled from that distribution is indeed okay ("secure enough").


"the idea of only serving clients confined to these benign query distributions undoubtedly assumes that whatever can be deduced about the model by a benign client using queries sampled from that distribution is indeed okay ('secure enough')."



To think about this deeper, let's focus on the case of OMEDs for ML classifiers (which output a prediction about whether some item (e.g. a picture) belongs to the " + " class or the " - " class). At a first glance, the theory of statistical learning (Vapnik and Chervonenkis) --- which tells us that a number of samples proportional to the VC dimension of the hypothesis class suffices for PAC-learning --- seems to end the hopes of using the current notion of security to obtain any meaningful protection.

This is because an adversary with unbounded computational power could simply query the model according to one of the appropriate distributions of random examples for a sufficient number of times, and then apply a PAC-learning algorithm (which is guranteed to exist by the fundamental theorem of statistical learning). The output of this algorithm would be a function which would be a strong approximation to the underlying ML model with high confidence.

What about computationally bounded adversaries?

However, this attack doesn't account for the complexity of the implied model extraction attack: depending on the complexity of the model, this type of attack may have superpolynomial query and computational complexity. For instance, for many important families of classifiers (e.g. boolean decision trees), no polynomial time PAC-learning algorithms are known, despite intense effort from the learning theory community. Actually, this is true even when the queries are restricted to being uniformly distributed, and the decision tree is "typical" (not only worst-case hard).

All in all, this adds evidence for the claim that the model of security implicitly considered by observational defenses might actually be effective in preventing unwanted model extraction by computationally bounded adversaries. The OMED forces the adversary to interact with the query interface in a way that mimics uniformly random examples, or some other distribution, from which it is hard to learn the underlying model.

Then, security against model extraction by computationally bounded adversaries can be provable in a complexity-theoretic way (like in Cryptography): one could hope to give a reduction from polynomial time PAC-learning to polynomial time model extraction in the presence of observational defenses. In other words, one could hope to prove a theorem that says "any efficient algorithm to learn an approximation of a proprietary ML model when constrained by an observational defense yields a PAC-learning algorithm (that is currently beyond all known techniques)."


"one could hope to give a reduction from polynomial time PAC-learning to polynomial time model extraction in the presence of observational defenses."



The contributions of [Kar23]

So we have established that OMEDs can be possibly used to obtain a notion of provable security against computationally bounded adversaries. The main question we tackle in [Kar23], is the natural follow-up: can OMEDs be efficiently implemented against these efficient adversaries?

In [Kar23], I provided a negative answer to this question. I did it via the following program:

Next time

In the next blog post, we will dig into what exactly is Covert Learning, and further illuminate the connection to model extraction.

References


[BCK+22] Eric Binnendyk, Marco Carmosino, Antonina Kolokolova, Ramyaa Ramyaa, and Manuel Sabin. Learning with distributional inverters. In International Conference on Algorithmic Learning Theory, pages 90–106. PMLR, 2022.
[BFKL93] Avrim Blum, Merrick Furst, Michael Kearns, and Richard J Lipton. Cryptographic primitives based on hard learning problems. In Annual International Cryptology Con- ference, pages 278–291. Springer, 1993.
[CCG+20] Varun Chandrasekaran, Kamalika Chaudhuri, Irene Giacomelli, Somesh Jha, and Song- bai Yan. Exploring connections between active learning and model extraction. In 29th {USENIX} Security Symposium ({USENIX} Security 20), pages 1309–1326, 2020.
[CJM20] Nicholas Carlini, Matthew Jagielski, and Ilya Mironov. Cryptanalytic extraction of neural network models. arXiv preprint arXiv:2003.04884, 2020.
[CK21] Ran Canetti and Ari Karchmer. Covert learning: How to learn with an untrusted intermediary. In Theory of Cryptography Conference, pages 1–31. Springer, 2021.
[CLP13] Kai-Min Chung, Edward Lui, and Rafael Pass. Can theories be tested? a cryptographic treatment of forecast testing. In Proceedings of the 4th conference on Innovations in Theoretical Computer Science, pages 47–56, 2013.
[DKLP22] Adam Dziedzic, Muhammad Ahmad Kaleem, Yu Shen Lu, and Nicolas Papernot. In- creasing the cost of model extraction with calibrated proof of work. arXiv preprint arXiv:2201.09243, 2022.
[GBDL+16] Ran Gilad-Bachrach, Nathan Dowlin, Kim Laine, Kristin Lauter, Michael Naehrig, and John Wernsing. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In International Conference on Machine Learning, pages 201–210. PMLR, 2016.
[GL89] Oded Goldreich and Leonid A Levin. A hard-core predicate for all one-way functions. In Proceedings of the twenty-first annual ACM symposium on Theory of computing, pages 25–32, 1989.
[GMR89] Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof systems. SIAM Journal on computing, 18(1):186–208, 1989.
[GPV08] Craig Gentry, Chris Peikert, and Vinod Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the fortieth annual ACM sym- posium on Theory of computing, pages 197–206, 2008.
[JCB+20] Matthew Jagielski, Nicholas Carlini, David Berthelot, Alex Kurakin, and Nicolas Paper- not. High accuracy and high fidelity extraction of neural networks. In 29th {USENIX} Security Symposium ({USENIX} Security 20), pages 1345–1362, 2020. 25
[JSMA19] Mika Juuti, Sebastian Szyller, Samuel Marchal, and N Asokan. Prada: protecting against dnn model stealing attacks. In 2019 IEEE European Symposium on Security and Privacy (EuroS&P), pages 512–527. IEEE, 2019.
[Kar23] Ari Karchmer. Theoretical limits of provable security against model extraction by efficient observational defenses. In 2023 IEEE Conference on Secure and Trustworthy Machine Learning (SaTML), pages 605–621. IEEE, 2023.
[KM93] Eyal Kushilevitz and Yishay Mansour. Learning decision trees using the fourier spec- trum. SIAM Journal on Computing, 22(6):1331–1348, 1993.
[KMAM18] Manish Kesarwani, Bhaskar Mukhoty, Vijay Arya, and Sameep Mehta. Model extrac- tion warning in mlaas paradigm. In Proceedings of the 34th Annual Computer Security Applications Conference, pages 371–380, 2018.
[KST09] Adam Tauman Kalai, Alex Samorodnitsky, and Shang-Hua Teng. Learning and smoothed analysis. In 2009 50th Annual IEEE Symposium on Foundations of Computer Science, pages 395–404. IEEE, 2009.
[Nan21] Mikito Nanashima. A theory of heuristic learnability. In Conference on Learning Theory, pages 3483–3525. PMLR, 2021.
[O’D14] Ryan O’Donnell. Analysis of boolean functions. Cambridge University Press, 2014.
[PGKS21] Soham Pal, Yash Gupta, Aditya Kanade, and Shirish Shevade. Stateful detection of model extraction attacks. arXiv preprint arXiv:2107.05166, 2021.
[Pie12] Krzysztof Pietrzak. Cryptography from learning parity with noise. In International Conference on Current Trends in Theory and Practice of Computer Science, pages 99–114. Springer, 2012.
[PMG+17] Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. Practical black-box attacks against machine learning. In Proceed- ings of the 2017 ACM on Asia conference on computer and communications security, pages 506–519, 2017.
[RWT+18] M Sadegh Riazi, Christian Weinert, Oleksandr Tkachenko, Ebrahim M Songhori, Thomas Schneider, and Farinaz Koushanfar. Chameleon: A hybrid secure compu- tation framework for machine learning applications. In Proceedings of the 2018 on Asia Conference on Computer and Communications Security, pages 707–721, 2018.
[TZJ+16] Florian Tram`er, Fan Zhang, Ari Juels, Michael K Reiter, and Thomas Ristenpart. Stealing machine learning models via prediction apis. In 25th {USENIX} Security Symposium ({USENIX} Security 16), pages 601–618, 2016.
[Vai21] Vinod Vaikuntanathan. Secure computation and ppml: Progress and challenges. https: //www.youtube.com/watch?v=y2iYEHLY2xE&ab_channel=TheIACR, 2021.
[YZ16] Yu Yu and Jiang Zhang. Cryptography with auxiliary input and trapdoor from constant-noise lpn. In Annual International Cryptology Conference, pages 214–243. Springer, 2016.